研究与评论:纯粹与应用雷竞技苹果下载物理学杂志
菜单ISSN: 2320 - 2459
ISSN: 2320 - 2459
Jagadamba Prasad Vishwakarma*还有南希·帕特尔
Gorakhpur大学数学与统计系，Gorakhpur-273009，印度。
收到日期:16/09/2013修订日期:20/09/2013接受日期:28/09/2013
更多相关文章请访问raybet01
利用自相似方法研究了在空间变轴向和方位磁感应分量影响下，低导电气体中发散圆柱激波的传播。介质的初始密度要么是均匀的，要么服从幂律。同样，初始磁感应的两个分量都被取为与对称轴距离的某次方的变化。激波后面的流场总能量由于瞬时或时间相关的能量输入而恒定或增加。研究了初始密度和气体比热比的变化对激波传播和激波后流场的影响。
激波，自相似流，可变初始密度，可变初始磁感应，可变能量输入，低导电性。
林(1]扩展了泰勒的分析[2强烈的球形爆炸对圆柱形壳体的影响。得到了有限能量突然释放产生的强圆柱激波半径的变化规律。将分析结果应用于高超声速飞行的情况，表明流星或高速导弹后的激波包线近似为抛物面。
由于在与激波有关的问题中普遍存在的高温下，气体被电离，电磁效应也可能是显著的。因此，对这一问题的完整分析应同时包括对气体动力流动和电磁场的研究。在轴向或方位磁感应作用下，圆柱形激波在导电气体中传播的研究与夹点效应、导线爆炸等实验有关。这个问题在均匀理想气体或非均匀理想气体中都被许多研究者所研究，例如Pai [3.]，科尔和格雷芬格[4]、樱井[5]、不丹[6]，克里斯特和赫利维尔[7]，黛布·雷[8， Vishwakarma和Yadav [9]。这些工作的一个基本假设是，激波在气体介质中传播是能量沿直线瞬时释放的结果。
虽然瞬时能量输入的假设被认为对大多数问题是足够的，但在有些过程中，尽管能量输入非常快，但可以认为是与时间相关的。随时间变化的能量输入的例子有电弧放电、导线爆炸现象和化学能释放(可能发生在两相爆轰中)。弗里曼(10]已经考虑了由可变能量输入引起的冲击波的传播。他特别注意圆柱对称的情况，因为它特别应用于爆炸导线形成圆柱火花通道的问题(Freeman和Craggs [11])。
在目前的工作中，我们研究了在空间可变的磁感应轴向分量和方位分量的影响下，由于时间依赖的能量输入，在低导电和均匀或非均匀气体中发散的圆柱激波的传播。激波前沿前后的介质假定为无粘性介质，并表现为热完美气体。假定气体的初始密度是均匀的，或随距离的某次方而变化。激波后流场的总能量不是恒定的，而是随着能量输入时间的增加而增加。假定震波前面的气体处于静止状态。不考虑粘度、热传导、辐射和重力的影响。得到了激波前缘与内膨胀面之间的流动变量分布，并研究了初始密度和比热比的变化对激波前缘与内膨胀面之间流动变量的影响。
基本方程与边界条件
给出了低导电气体在轴向和方位磁感应分量作用下的非定常圆柱对称运动的基本方程(Tyl [12]、樱井[5和Vishwakarma [13]）
在哪里
分别为距离对称轴r处和时间t处的密度、速度、压力、轴向磁感应和方位磁感应，
为初始轴向磁感应，
初始方位磁感应，γ为比热比，μ为磁导率，σ为电导率，a为声速
气体单位质量的热力学能e由
假设，由于沿对称轴的爆炸，产生圆柱形激波，并在存在轴向磁感应的情况下传播到密度为ï ²0的低导电气体中和方位磁感应
假定气体的密度以及冲击前磁感应的轴向分量和方位分量是变化的，并遵循以下规律:
其中R为激波半径，A， α， S, Q, m, n为常数。
由于σ很小，磁感应可以连续地穿过激波前缘(Sakurai[5])。忽略反压力，冲击条件可以写成
下标s指的是激波前沿后面的条件和
表示激波的速度。
为了获得相似解，我们将未知变量写成以下形式(Vishwakarma和Yadav [9]）
f D P b在哪z，和b是无量纲变量的函数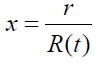
只有。激波锋用x = 1表示。
激波后流场的总能量不是恒定的，而是随时间变化的(Rogers [14]，弗里曼[10]、董事及达博拉[15])。
(3.2)
在E0k是常数。k的正值对应的是总能量随时间增加的类别。由于流动是绝热的，激波很强，这种增加只能通过膨胀表面(接触面或活塞)施加在流体上的压力来实现。雷竞技网页版在电线爆炸形成圆柱形火花通道的过程中，也可能出现类似的情况。此外，在火花击穿的通常情况下，与瞬时能量输入相比，时间相关的能量输入是一个更现实的假设(Freeman [10])。
激波前缘与内膨胀面(活塞)之间流动的总能量因此表示为
(3.3)
在rp是内曲面的半径。
应用关系式(3.3)中的相似变换(3.1)，我们发现激波锋的运动由方程给出
(3.4)
在哪里
xp是内膨胀面上x的值。
式(3.4)积分得到
因此,
将式(2.1)~式(2.5)进行相似变换后，变为常微分方程
在哪里
分别为磁雷诺数、轴向阿尔芬-马赫数和方位阿尔芬-马赫数，分别为
利用自相似变换(3.1)，边界条件(2.10)可以写成
对于相似解的存在性，磁雷诺数R米，轴向阿尔芬马赫数M阿兹方位阿尔芬马赫数MAA¯±应该是常数。因此,
在哪里
通过求解式(3.7)到式(3.9)得到
我们得到了
在内膨胀面上需要满足的条件是流体的速度等于表面本身的速度。这个运动学条件，可以写成
为了显示数值解，可以方便地将字段变量写成如下形式:
这些变量的激波边界条件是
现在可以将微分方程(3.10)、(3.11)、(3.14)到(3.16)与边界条件(3.12)进行数值积分，得到激波前缘与内膨胀面之间的流场。
减少的流量变量
由微分方程(3.10)、(3.11)、(3.14)到(3.16)在边界条件(3.12)下的数值积分得到。为了数值积分，取常数参数的值为(Vishwakarma and Singh [16]) γ = 1.4,1.66;
α = 0对应于均匀密度气体中瞬时能量释放(k = 0)产生激波的情况。
数字1 - 5显示流量变量的变化
x在不同的α和γ参数值下。结果表明，当我们从激波前缘向内膨胀面移动时，流体速度减小
α值越低(= 0,0.5)，则越低;α值越高(= 1.5,2.0)，则越高;密度降低了
减压
降低了轴向磁感应
α的所有可接受值均降低，而方位磁感应降低
增加。表1表示内膨胀面x的无因次位置p在不同的α和γ值。
密度变化指数α增加的影响是(从数字1 - 5）：
(i)增加速度还有压强在激波后面流场中的任意一点;
(ii)降低密度还有轴向磁感应
(iii)减小速度和压力剖面的斜率，增大密度和轴向磁感应剖面的斜率;和
(iv)减小距离(1−x)p)内膨胀面与激波前缘(见表1）.这意味着内膨胀面速度与激波前缘速度之比增大，导致激波后气体压缩增大，激波强度增大。
事实上，随着α的增加，k增加，这增加了随时间变化的能量输入(通过式(3.2))，导致内膨胀面的速度增加，从而增加了激波强度。γ的增加的影响是(从数字1 - 5）：
(i)降低速度为了增加密度还有轴向磁感应在激波后面流场中的任意一点;
(ii)减小密度剖面和轴向磁感应剖面的斜率;和
(iii)稍微增加内膨胀面到激波前沿的距离(表1）.
α或γ的变化对方位角磁场没有影响
在激波后面的流场中。
由式(3.5)(3.13)可知，激波速度Ã Â R随时间减小，随t变化−1/2。
表1。内膨胀面x的位置p在不同的α和γ值下
和R米= 0.01。
图1所示。
图2。
图3。
图4。
图5。
本文得到了圆柱形激波在低导电气体中在不同初始磁感应轴向分量和方位角分量影响下传播的相似解。根据目前的研究，我们可以得出以下结论:
(i)激波速度随时间而减小，t−1/2。
(ii)密度变化指数α值增大，速度增大在压强下，密度减小以及轴向磁感应在激波后面流场中的任意一点。
(iii) α的增加，增加了随时间变化的能量输入，从而增加了冲击强度。
iv) γ值的增加引起密度的增加以及轴向磁感应，速度减小在激波后面流场中的任意一点。
